Welches Bundesland produziert die dümmsten Mathematikaufgaben: Baden-Württemberg oder Nordrhein-Westfalen?
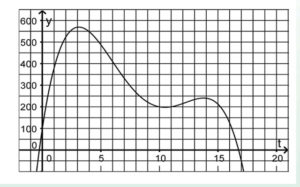
Franz Lemmermeyer nimmt in seinem Artikel “Don’t know what a slide rule is for” eine Musteraufgabe für ein Mathematikabitur in Baden-Württemberg auseinander. Die Aufgabe enthält den Graphen einer Funktion f (siehe Abbildung).
Eine Teilaufgabe lautet:
Begründen Sie, dass die Funktionsgleichung von f weder die Form I noch die Form II hat:
(I)
(II).
Lemmermeyer kommentiert das so:
Hier muss man schreiben, dass das Schaubild von f nicht symmetrisch zur y-Achse
ist und drei Extrempunkte hat, was I und II ausschließt. Das ist so ungefähr wie wenn man im Deutsch-Abitur zeigen soll, dass beiFest gemauert in der Erden
Steht die Form, aus Lehm gebrannt.
Heute muss die Glocke werden.
Frisch Gesellen, seid zur Hand.das Reimschema nicht AABB ist. Oder in Astronomie, dass der Vollmond nicht aussieht wie ein Quadrat. Nein, nicht wirklich. Eigentlich ist es kaum möglich, in einem andern Fach eine Aufgabe zu entwerfen, die genauso bescheuert ist wie diese hier. Das geht echt nur in Mathematik. Und in Baden-Württemberg.
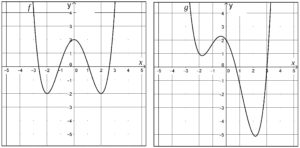
Wir müssen hier entschieden widersprechen. Aufgaben, die so bescheuert und anspruchslos sind, gibt es nicht nur in Baden-Württemberg, sondern auch in Nordrhein-Westfalen. Zum Beispiel in der zentralen Klausur für Mathematik 2017 am Ende der Einführungsphase1. Da waren zwei Funktionen, ![]() und
und ![]() , und deren jeweiliger Graph gegeben (siehe Abbildung).2
, und deren jeweiliger Graph gegeben (siehe Abbildung).2
Eine Teilaufgabe lautete (– Achtung, festhalten!):
Nennen Sie zwei Unterschiede der Graphen von
und
.
Die Musterlösung macht es unnötig kompliziert:
Beispiele für Unterschiede:
- Der Graph von f ist achsensymmetrisch zur y-Achse, der Graph von g weist keine Symmetrie auf.
- Beim Graphen von f stimmen die y-Koordinaten der beiden Tiefpunkte überein, beim Graphen von g unterscheiden sich die y-Koordinaten der beiden Tiefpunkte.
- Beim Graphen von f sind die y-Koordinaten aller Extrempunkte ganzzahlig, beim Graphen von g sind die y-Koordinaten der Extrempunkte nicht ganzzahlig.
- Die y-Koordinaten aller Punkte auf dem Graphen von f sind größer oder gleich -2, es gibt Punkte auf dem Graphen von g, deren y-Koordinaten kleiner als -2 sind.
- Der Graph von f schneidet die x-Achse in vier Punkten, der Graph von g schneidet die x-Achse nur in zwei Punkten.
Wir erkennen folgende Unterschiede:
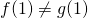 ,
,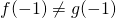 ,
,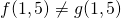 .
.
Nebenbei: Dass es Schüler gab, die mit so einer Aufgabe nichts anfangen konnten, weil sie dermaßen simpel und somit ungewohnt war, halten wir nicht für ausgeschlossen. Aber für 2018 wissen die Lehrer ja jetzt, worauf sie die Schüler abrichten — ähm, sorry — trainieren müssen. Zum Einstieg in das Thema “Unterschiede zwischen Funktionsgraphen” schlagen wir diese Aufgabe vor:
Abgebildet sind zwei Personen. Nennen Sie zwei Unterschiede!

Fazit: Was bescheuerte Mathematikaufgaben angeht, braucht das Land Nordrhein-Westfalen keinen Vergleich scheuen, schon gar nicht den Vergleich mit Baden-Württemberg.
——————-
- erstes Schuljahr der gymnasialen Oberstufe, also 10. oder 11. Schuljahr, je nachdem ob G8-Gymnasium oder Gesamtschule
- Die vollständige Klausur samt Lösung gibt es in dem Buch “Zentrale Klausur Gymnasium NRW – Mathematik. 2018” aus dem Stark-Verlag. Alternativ kann man auf diese Seite des Schulministeriums gehen. Die notwendigen Login-Daten findet man beispielsweise hier.